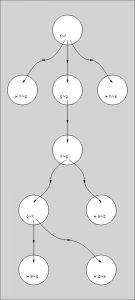
Introduction

De façon classique, pour linéariser une matrice de n x n, on utilise une formule telle que :

indice(x, y) ↦ x + y * n

et inversement, coordonnées(i) ↦ { i mod n, i div n }

Avec mod : le modulo, et div la division entière, qui utilise le fait que la division euclidienne est une bijection entre les entiers positifs ou nuls et les couples d’entiers positifs ou nuls.

Par exemple, pour matrice de 3 x 3, les indices dans la table linéaire peuvent être :

Figure 1

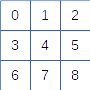
Tout dépend des choix, ligne/colonnes, sens droite/gauche, haut bas, etc. Mais cela dépend essentiellement de la taille de la matrice :

Figure 2

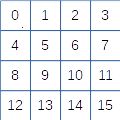
Pour la taille 4 x 4, avec les mêmes choix d’orientation, seules 3 cases gardent la même place.

Le problème est donc : si la matrice grandit la version linéaire de la matrice est à recalculer.

Proposition

Figure 3

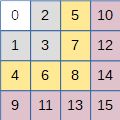
Dans le cas de matrices carrées pouvant être amenée à grandir, par exemple si celles-ci représentent les matrices d’incidence de graphes auxquels on ajoute de nouveaux sommets, je propose une numérotation « incrémentale » ne changeant pas les indices si la matrice croît.

Numérotation triangulaire

Figure 4

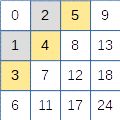
La numérotation triangulaire est une bijection possible, mais elle laisse des trous. Par exemple dans la matrice de 2 x 2, l’indice 3 n’est pas utilisé, et c’est de pire en pire en augmentant la taille.

Méthode de rangement

On propose de générer les indices en partant d’un carré de 1, puis en ajoutant une ‘couche’ de 2n + 1 éléments à chaque incrémentation de n. Les couches sont représentées par les couleurs dans la figure 3.

Nommons indices, les indices i de la forme linéaire, et coordonnées les couples (x, y) donnant la position dans la forme matricielle.

On s’arrange pour que :

1/ Si les coordonnées x et y varient de 0 à n – 1, alors les indices i correspondants varient de 0 à n² -1.

2/ Le plus grand indice dans un carré de n corresponde au plus grand couple de coordonnées.

Donc, les indices des éléments de la diagonale principale, de coordonnées (x, y) avec x === y, valent (x + 1)² – 1. Ce qui donne la suite : 0, 3, 8, 15…

3/ On garantit que si x et y sont tous deux inférieurs à n, l’indice de (x, y) sera inférieur à n².

4/ Et enfin, on garantit que tous les indices déterminés au niveau du carré de n seront toujours valables dans un carré de n+1, et récursivement en partant de n = 1.

Notation

Il faut choisir une orientation pour représenter les figures, la voici :

Figure 5

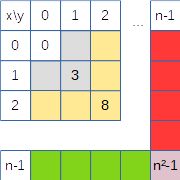
Les lignes sont numérotées x et les colonnes y. Le gnomon du carré est décomposé en trois parties : la diagonale de surface 1, notée avec son indice n² – 1, la partie rouge avec y = n – 1 qu’on peut nommer le gnomon de y, et le gnomon de x, en vert, avec x = n – 1.

Implémentation

Sous forme de fonctions :

function index(x, y) {
	if (x === y) {
		return (x + 1) * (x + 1) - 1;
	}
	// retrouver le plus petit carré contenant (x, y)
	n = Math.max(x, y);
	if (x > y) {
		// on est dans le gnomon de x
		return n * n + 2 * y;
	}
	// sinon, y > x
	return n * n + 1 + 2 * x;
}

function coordonnées(i) {
	// retrouver n
	let r = Math.sqrt(i + 1);
	if (Number.isInteger(r)) {
		// on est sur la diagonale
		return { x: r - 1, y: r - 1 };
	}
	let n = Math.floor(r);
	let k = i - n * n;
	if (k & 1) {
		// impair : gnomon de y
		return { x: (k - 1) / 2, y: n};
	}
	// pair : gnomon de x
	return { x: n, y: k / 2};
}

Si on préfère on peut aussi utiliser une mémo-fonction pour établir les correspondances. On doit choisir entre temps de calcul ou utilisation de mémoire selon les cas.

function index(x, y) {
	if (x === y) {
		// on est dans la diagonale 
		return (x + 1) * (x + 1) - 1;
	}
	if (x > y) {
		// on est dans le gnomon de x
		return x * x + 2 * y;
	}
	// sinon, y > x, on est dans le gnomon de y
	return y * y + 1 + 2 * x;
}

Bien sûr on peut simplifier la fonction index comme ci-dessus. On n’est pas obligés de calculer n.

x\y	0	1	2	3	4	5	6	7	8	9	10
0	0	2	5	10	17	26	37	50	65	82	101
1	1	3	7	12	19	28	39	52	67	84	103
2	4	6	8	14	21	30	41	54	69	86	105
3	9	11	13	15	23	32	43	56	71	88	107
4	16	18	20	22	24	34	45	58	73	90	109
5	25	27	29	31	33	35	47	60	75	92	111
6	36	38	40	42	44	46	48	62	77	94	113
7	49	51	53	55	57	59	61	63	79	96	115
8	64	66	68	70	72	74	76	78	80	98	117
9	81	83	85	87	89	91	93	95	97	99	119
10	100	102	104	106	108	110	112	114	116	118	120

Tableau 1 : Les index placés à leur coordonnées pour n = 11.