Le Maestro est sur Apple music

Écoutez les dernières musiques publiées sur Apple music.
Introduction
De façon classique, pour linéariser une matrice de n x n, on utilise une formule telle que :
indice(x, y) ↦ x + y * n
et inversement, coordonnées(i) ↦ { i mod n, i div n }
Avec mod : le modulo, et div la division entière, qui utilise le fait que la division euclidienne est une bijection entre les entiers positifs ou nuls et les couples d’entiers positifs ou nuls.
Par exemple, pour matrice de 3 x 3, les indices dans la table linéaire peuvent être :
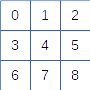
Tout dépend des choix, ligne/colonnes, sens droite/gauche, haut bas, etc. Mais cela dépend essentiellement de la taille de la matrice :
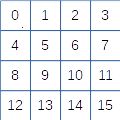
Pour la taille 4 x 4, avec les mêmes choix d’orientation, seules 3 cases gardent la même place.
Le problème est donc : si la matrice grandit la version linéaire de la matrice est à recalculer.
Proposition

Dans le cas de matrices carrées pouvant être amenée à grandir, par exemple si celles-ci représentent les matrices d’incidence de graphes auxquels on ajoute de nouveaux sommets, je propose une numérotation « incrémentale » ne changeant pas les indices si la matrice croît.
Numérotation triangulaire
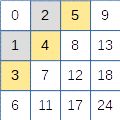
La numérotation triangulaire est une bijection possible, mais elle laisse des trous. Par exemple dans la matrice de 2 x 2, l’indice 3 n’est pas utilisé, et c’est de pire en pire en augmentant la taille.
Méthode de rangement
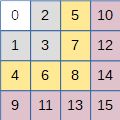
On propose de générer les indices en partant d’un carré de 1, puis en ajoutant une ‘couche’ de 2n + 1 éléments à chaque incrémentation de n. Les couches sont représentées par les couleurs dans la figure 3.
Nommons indices, les indices i de la forme linéaire, et coordonnées les couples (x, y) donnant la position dans la forme matricielle.
On s’arrange pour que :
1/ Si les coordonnées x et y varient de 0 à n – 1, alors les indices i correspondants varient de 0 à n² -1.
2/ Le plus grand indice dans un carré de n corresponde au plus grand couple de coordonnées.
Donc, les indices des éléments de la diagonale principale, de coordonnées (x, y) avec x === y, valent (x + 1)² – 1. Ce qui donne la suite : 0, 3, 8, 15…
3/ On garantit que si x et y sont tous deux inférieurs à n, l’indice de (x, y) sera inférieur à n².
4/ Et enfin, on garantit que tous les indices déterminés au niveau du carré de n seront toujours valables dans un carré de n+1, et récursivement en partant de n = 1.
Notation
Il faut choisir une orientation pour représenter les figures, la voici :
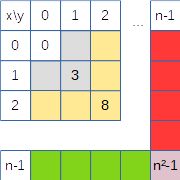
Les lignes sont numérotées x et les colonnes y. Le gnomon du carré est décomposé en trois parties : la diagonale de surface 1, notée avec son indice n² – 1, la partie rouge avec y = n – 1 qu’on peut nommer le gnomon de y, et le gnomon de x, en vert, avec x = n – 1.
Implémentation
Sous forme de fonctions :
function index(x, y) {
if (x === y) {
return (x + 1) * (x + 1) - 1;
}
// retrouver le plus petit carré contenant (x, y)
n = Math.max(x, y);
if (x > y) {
// on est dans le gnomon de x
return n * n + 2 * y;
}
// sinon, y > x
return n * n + 1 + 2 * x;
}
function coordonnées(i) {
// retrouver n
let r = Math.sqrt(i + 1);
if (Number.isInteger(r)) {
// on est sur la diagonale
return { x: r - 1, y: r - 1 };
}
let n = Math.floor(r);
let k = i - n * n;
if (k & 1) {
// impair : gnomon de y
return { x: (k - 1) / 2, y: n};
}
// pair : gnomon de x
return { x: n, y: k / 2};
}
Si on préfère on peut aussi utiliser une mémo-fonction pour établir les correspondances. On doit choisir entre temps de calcul ou utilisation de mémoire selon les cas.
function index(x, y) {
if (x === y) {
// on est dans la diagonale
return (x + 1) * (x + 1) - 1;
}
if (x > y) {
// on est dans le gnomon de x
return x * x + 2 * y;
}
// sinon, y > x, on est dans le gnomon de y
return y * y + 1 + 2 * x;
}
Bien sûr on peut simplifier la fonction index comme ci-dessus. On n’est pas obligés de calculer n.
|
x\y |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
0 |
0 |
2 |
5 |
10 |
17 |
26 |
37 |
50 |
65 |
82 |
101 |
|
1 |
1 |
3 |
7 |
12 |
19 |
28 |
39 |
52 |
67 |
84 |
103 |
|
2 |
4 |
6 |
8 |
14 |
21 |
30 |
41 |
54 |
69 |
86 |
105 |
|
3 |
9 |
11 |
13 |
15 |
23 |
32 |
43 |
56 |
71 |
88 |
107 |
|
4 |
16 |
18 |
20 |
22 |
24 |
34 |
45 |
58 |
73 |
90 |
109 |
|
5 |
25 |
27 |
29 |
31 |
33 |
35 |
47 |
60 |
75 |
92 |
111 |
|
6 |
36 |
38 |
40 |
42 |
44 |
46 |
48 |
62 |
77 |
94 |
113 |
|
7 |
49 |
51 |
53 |
55 |
57 |
59 |
61 |
63 |
79 |
96 |
115 |
|
8 |
64 |
66 |
68 |
70 |
72 |
74 |
76 |
78 |
80 |
98 |
117 |
|
9 |
81 |
83 |
85 |
87 |
89 |
91 |
93 |
95 |
97 |
99 |
119 |
|
10 |
100 |
102 |
104 |
106 |
108 |
110 |
112 |
114 |
116 |
118 |
120 |
Tableau 1 : Les index placés à leur coordonnées pour n = 11.
Thème musical
Thème musical rendu algorithmique
Algorithmique est un bien grand mot, je pars d’une ancienne improvisation que j’avais retranscrite en 2006, et j’analyse sa construction. Je sors principalement l’aspect rythmique et le mouvement mélodique sans préoccupation d’harmonie.
J’en fait une « procédure » à suivre pour construire un thème de base à développer et orchestrer ensuite.
La mesure est à 6/8.
On choisit un mode, mineur par exemple.
Voix de basse
On choisit deux accords dans le mode, dont on extrait 3 sons, avec au moins une note commune entre les deux groupes de trois sons.
En arpégeant, de bas en haut, on en fait 6 croches, c’est-à-dire une mesure :

Module A, à la basse, avec une note commune dans a0 ⋂ a1 de préférence en position 3 dans les groupes.
Voix mélodique
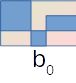
On construit un groupe b0, d’une durée de 5 croches, avec deux hauteurs pour former trois notes.
La première, noire est accentuée, la seconde est une croche plus basse et la troisième note est une noire de la même hauteur que la première mais moins forte.
Ce groupe b0 sera répété 2 fois dans le module B, introduisant un décalage rythmique par l’anomalie des 5 unités au lieu de 6.

Un second groupe b1 est en réponse et conclusion de la répétition de b0. Il se démarque en commençant plus haut que b0. Il répond à b0 en inversant le mouvement sur la hauteur de la seconde note tout en reprenant le même rythme et la même répétition de la première hauteur en troisième position. Il est conclusif par la descente finale, mais pas tout à fait, la dernière note doit se résoudre sur la première de b0. par exemple être la même hauteur que la seconde note de b0.
Le groupe b1 a une durée de 8 croches, comme dans les rythmes binaires alors que la mesure est ternaire. Mais comme dans une rumba, 8 et décomposé en 3 + 3 + 2, se rapprochant du ternaire avec un manque.
Et finalement, on retombe sur ses pieds parce que 2 x 5 + 8 = 18 = 3 x 6.
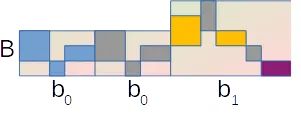
Le module C est une répétition de 3 fois un groupe de 4 noires.

Comme il arrive après B, on est déjà dans le bain d’un binaire chevauchant le ternaire de la basse. On peut voir la suite b1, c0, c0, c0, comme 4 mesures à 4 temps. Par rapport au stress à la croche de la basse ternaire, il est deux fois plus lent.
Thème complet
Enfin on assemble le tout :
une sorte d’anacrouse de A x 2 pour démarrer, puis deux fois (X x 2 suivit de Y).

Les répétitions font varier légèrement les accentuations.
13/11/2021

Pour les nostalgiques de Phonogramme et Sonographe, je vous présente une page web permettant de dessiner des sons, de les écouter et les enregistrer.
https://www.cyclonium.com/atelier/synthese/sonographeParallele.html
C’est une préfiguration de ce que pourrait être un ‘SoundPaint’ dans une page web. Pour l’instant, c’est une maquette, en développement, mais elle permet déjà de dessiner et écouter, quasiment en temps réel.
En fait, il faut environ 2 secondes pour calculer 30 secondes de son, grâce à notre bibliothèque de calcul parallèle basée sur WebGL (Paradigma).
La touche F12 remplace la documentation, il faut juste lire le code.

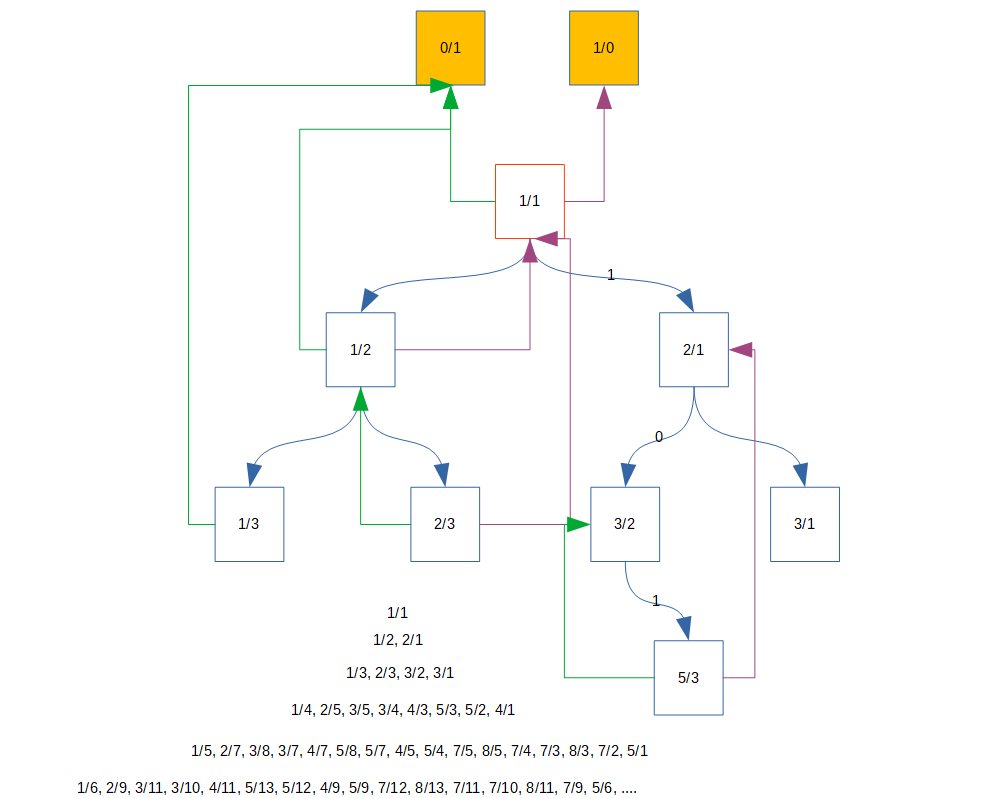
Une page d’expérimentation sur les fractions, représentées par un couple de grands entiers, maintenant accessibles en JavaScript sous le nom de BigInt.


Cet article présente une simulation de balance de Roberval pour apprendre les bases de numération de position.
Il suffit de cliquer sur les poids pour équilibrer la balance. Une fois l’équilibre atteint, le nombre de billes est écrit sous le plateau de gauche dans la base choisie.
La documentation complète est dans la page d’expérience. Cliquez sur l’image pour démarrer.

Un jeu d’enfant, l’instrument concocté par Ian Snyder est très simple et intuitif.
Un élastique et 6 punaises délimitent 5 cordes vibrantes.
La longueur des cordes correspond (à une transformation près) à la hauteur du son : comme en vrai, plus la corde est longue plus le son est grave et inversement, plus la corde est courte plus le son correspondant est aigu.
Pour faire sonner une corde, il suffit de l’attraper à la souris, de tirer dessus et de la relâcher. L’intensité du son produit est corrélé à la traction effectuée avant de relâcher : plus on tire, plus le son est fort.
En haut à gauche, le bouton « tuning » permet d’accorder l’instrument selon plusieurs gammes :
Un bout de commentaire dans le code correspondant :
// all – [1,1,1,1,1,1,1,1,1,1,1,1]
// penta – [1,0,1,0,1,0,0,1,0,1,0,0]
// hexa – [1,0,1,0,1,0,1,0,1,0,1,0]
// hepta – [1,0,1,0,1,1,0,1,0,1,0,1]
// octa – [1,1,0,1,1,0,1,1,0,1,1,0]
/* A BC D EF G
000000000000
1-1-1-1-1-1- > whole
–11–11–11 > augmented
11-1-1-1-1– > prometheus
-1-1–1-111- > blues
> 1–1-1-11-1- > diatonic
*/
Le code en vrai dans la fonction tuneMode() :
switch (tuning) {
case 1:
scale = [1,1,1,1,1,1,1,1,1,1,1,1];
str = "12 tone";
break;
case 2:
scale = [1,1,0,1,1,0,1,1,0,1,1,0];
str = "8 tone";
break;
case 3:
scale = [1,0,1,0,1,1,0,1,0,1,0,1];
str = "7 tone";
break;
case 4:
scale = [1,0,1,0,1,0,1,0,1,0,1,0];
str = "6 tone (whole)";
break;
case 5:
scale = [1,1,0,0,1,1,0,0,1,1,0,0];
str = "6 tone (augmented)";
break;
case 6:
scale = [1,1,0,1,0,1,0,1,0,1,0,0];
str = "6 tone (prometheus)";
break;
case 7:
scale = [0,1,0,1,0,0,1,0,1,1,1,0];
str = "6 tone (blues)";
break;
case 8:
scale = [1,0,0,1,0,1,0,1,1,0,1,0];
str = "6 tone (diatonic)";
break;
case 9:
scale = [1,0,1,0,1,0,0,1,0,1,0,0];
str = "5 tone";
break;
}
On est toujours basé sur une échelle en 12 demi-tons, à moins de mettre le « tuning » à OFF.
On peut changer le timbre utilisé : il suffit de choisir le fichier d’échantillons à utiliser (en wav, mp3, etc…) disponible sur sa machine.
Par exemple, un son de corde de violoncelle : téléchargez
https://www.cyclonium.com/atelier/sons/Cello.wav
Ou encore un son produit par SoundPotatoes :
https://www.cyclonium.com/atelier/sons/Potato20200828_7b.mp3
Vous avez remarqué que les mouvements effectués à la souris sont répétés automatiquement, à intervalle de temps réguliers. En bas à gauche le bouton : SWARM permet de régler les répétitions des mouvements. Pas de répétition, ou 2, 4, 8, 16, 32 et 64 répétitions (tiens ! des puissances de deux).
Les répétitions des mouvements concernent là la fois le jeu sur les cordes et le déplacement des punaises.
Enfin, le bouton « Snapping » en haut à gauche montre que Ian s’est également intéressé aux grilles hexagonales. Si le « Snapping » est actif, les positions des punaises sont ajustées à la grille.

Constellations est un jeu, un puzzle, inventé par Ian Snyder et programmé par lui-même en HTML 5 dans un « canvas » 2D.
Il s’agit de résoudre les puzzles en manipulant des élastiques accrochés à des punaises : pour le faire il suffit de reproduire le schéma linéaire des tensions, accroches et croisements proposé en haut de l’écran.
Le niveau que vous avez atteint est stocké dans le « localStorage » du navigateur de sorte que si vous revenez sur la page, les puzzles résolus ne seront proposés qu’en utilisant le bouton « back » en bas à gauche. Le bouton « skip » permet d’abandonner un puzzle pour s’attaquer au suivant.
Pour les sons, Ian Snyder utilise la bibliothèque « howler.js » (https://howlerjs.com/) développée par James Simpson. C’est dommage qu’il utilise une ancienne version de la bibliothèque, car les règles ont changé depuis 2018 : on ne peut plus utiliser l’API Audio avant que l’utilisateur n’ait interagit avec la page. Du coup, on risque de ne pas avoir de sons. (pour remédier au problème, il faut remplacer le fichier * howler.js v2.0.3 ) par le fichier * howler.js v2.2.0) Dans la console de développement sous Google Chrome (touche F12) on peut lire le message :
The AudioContext was not allowed to start. It must be resumed (or created) after a user gesture on the page. https://goo.gl/7K7WLu
setupAudioContext @ howler.js:2133
Références
Lien vers une version sonore : https://www.cyclonium.com/ianestailleurs/constellations/
Jouer à Constellations : http://ianiselsewhere.com/constellations/
Voir le site de Ian Snyder : http://iansnyder.games/
L’article de « Libération » sur le sujet : https://www.liberation.fr/futurs/2018/03/26/constellations-la-musique-de-l-elastique_1638964
Note pour les programmeurs JavaScript
À noter dans le code, au hasard des lignes, pour choisir un son au hasard parmi 9 disponibles, Ian Snyder utilise la formule compacte :
1+((Math.random()*9)|0)
au lieu d’un plus clasique 1+Math.floor(Math.random()*9)
L’explication est qu’en JavaScript, l’opérateur « | » (ou inclusif binaire) n’opère que sur des entiers. Le résultat de (Math.random()*9) est donc tronqué à sa partie entière avant de passer par le « ou » avec zéro, qui évidemment conserve les bits en l’état. L’écriture est plus courte et on évite un appel de fonction.
L’envers du Tricérata